LeetCode

Subtree of Another Tree

Approach 1: Brute Force ⭐

For every node in the bigger tree s, we want to check if it is the same tree as the smaller tree t. We use recursion to accomplish this:

If the current node in s is the same tree as t, return true
Otherwise, recursively check if the current node’s left child contains t as a subtree or if the current node’s right child contains t as a subtree

For more details or alternate implementations of isSameTree(), check out my explanation of LeetCode problem Same Tree.

Complexity Analysis

Let m = number of nodes in s
Let n = number of nodes in t

Time: \(O(mn)\)

In the worst case scenario, there are many duplicate values in s and t and we must check every node in t for every node in s.

Space: \(O(m)\)

Each recursive call takes up a stack frame and the worst case scenario occurs when s is skewed. Imagine we are \(m-x\) recursive calls deep into isSubtree() when isSameTree() is called. It takes at most \(x+1\) recursive calls of isSameTree() to reach a null child in s and verify that the current node is not t. Therefore, we will never use more than \(m+1\) stack frames.

Approach 2: Reduction to Substring Problem (String, indexOf) ⭐

Another approach to this problem is to reduce it to the substring problem first. The algorithm for this approach consists of 3 steps:

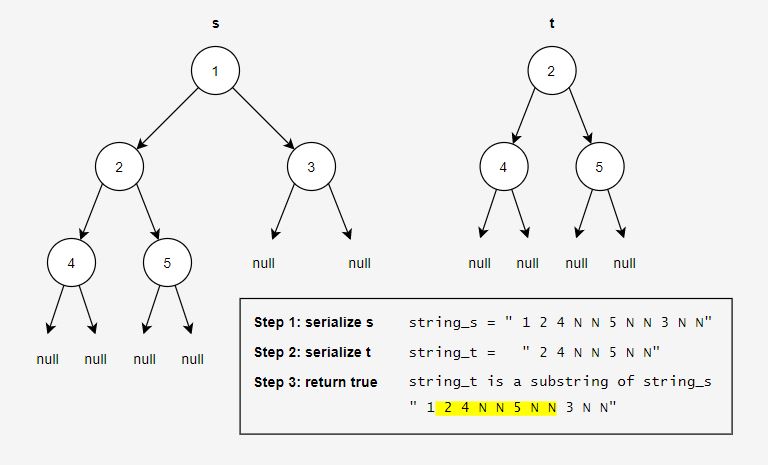
Serialize s - traverse the bigger tree s and store the order of the traversal in string_s
Serialize t - traverse the smaller tree t and store the order of the traversal in string_t
Return whether or not string_t is a substring of string_s

Things to note:

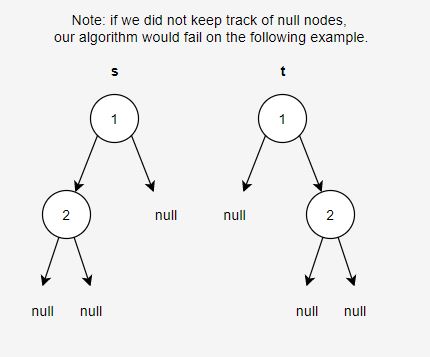
When we serialize a tree, we will use “N” to represent a null child.
When we serialize a tree, we will use a space “ “ as a delimiter in the strings to separate node values.
When we serialize a tree, we will traverse the nodes using a preorder traversal. If an inorder traversal or a postorder traversal is used instead, we would need to differentiate between left null children and right null children.
When checking whether string_t is a substring of string_s, we will use Java’s built in library function indexOf(), which returns the index of the first occurrence of string_t in string_s, and -1 otherwise.

Here is how the algorithm would work on the following input:

Here is an explanation for some of the bullet points above:

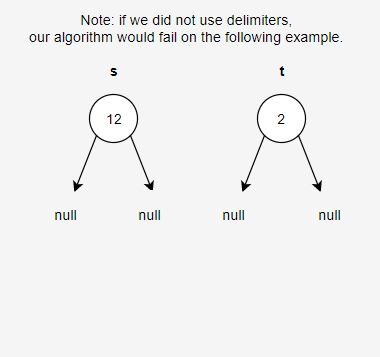
Below is the full solution:

Complexity Analysis

Let m = number of nodes in s
Let n = number of nodes in t

Time: \(O(m^2+n^2+mn)\)

With the code above, serializing s takes \(O(m^2)\) time. This is because String objects are immutable in Java. Therefore, when we append to the string \(m\) times, we are actually creating \(m\) new strings, each with length \(O(m)\). Initializing a string of length \(O(m)\) takes \(O(m)\) time, so initializing \(m\) strings of length \(O(m)\) takes \(O(m^2)\) time. This same reasoning is why serializing t takes \(O(n^2)\) time. Lastly, the Java library function indexOf() takes \(O(mn)\) time. This is because it uses a simple brute force substring algorithm.

Space: \(O(m^2+n^2)\)

Again, because strings are immutable in Java, we will end up creating \(m\) strings of length \(O(m)\) and \(n\) strings of length \(O(n)\). This will require \(O(m^2)\) and \(O(n^2)\) space respectively. In addition, serializing s and t require \(O(m)\) and \(O(n)\) stack frames, but this is negligible compared to the space required to store the strings.

Approach 3: Reduction to Substring Problem (StringBuilder, indexOf) ⭐

Using immutable strings was the primary cause of the previous approach’s bad time and space complexity. So let us use something mutable like StringBuilder or StringBuffer instead:

Complexity Analysis

Let m = number of nodes in s
Let n = number of nodes in t

Time: \(O(mn)\)

The limiting factor of the runtime for this algorithm comes from the Java library function indexOf(), which takes \(O(mn)\) time. Serializing s and t now only take \(O(m)\) and \(O(n)\) time respectively.

Space: \(O(m+n)\)

We need \(O(m)\) space to store one StringBuilder and one String of length \(m\), and we need \(O(n)\) space to store one StringBuilder and one String of length \(n\). In addition, serializing s and t require \(O(m)\) and \(O(n)\) stack frames respectively.

Approach 4: Reduction to Substring Problem (StringBuilder, KMP) ⭐⭐

We can improve the asymptotic runtime of the previous approach even further by using a linear time pattern searching algorithm instead of the library function indexOf(). I have chosen to use KMP as my linear time substring algorithm below:

Note that typically KMP finds all occurrences of a substring in a string, but I have modified it to return true as soon as it finds one occurrence.

Complexity Analysis

Let m = number of nodes in s
Let n = number of nodes in t

Time: \(O(m+n)\)

Space: \(O(m+n)\)

Optimization Ideas:

asdasd Morris Traversal

Approach 5: HashSet

Complexity Analysis

Let m = number of nodes in s
Let n = number of nodes in t

Time: \(O(m^2)\)

Space: \(O(m^2)\)